#2 Fitting Distributions (Baggage Handling System)

14:540:384: Simulation Models in IE (Spring 2025)

Author

Daniel Moore

Published

January 29, 2025

Questions

Learning Objectives

Create a Quarto Project
Install and load packages
Read data to tibble
Do basic plotting of the data
Fit a distribution to the data
Plot results

1 Problem

fictional

Newark Liberty International Airport is replacing Terminal B as part of their redevelopment plan. Daifuku has been selected to design the baggage handling system around which the terminal will be built. They have used their proprietary software, Sym3 to demonstrate that they meet the Port Authority’s specification documents for 60% Schematic Design.

Does the data indicate that bags will be delivered within 30 min +/- 5 min?

1.1 Start R Studio

1.2 Load Necessary Packages

Code

install.packages("tidyverse")
install.packages("knitr")
install.packages("fitdistrplus")

library(tidyverse)
library(knitr)
library(fitdistrplus)

1.3 Download Data

Airline Arrival data Bureau of Transportation Statistics
Simulated Baggage data: https://tinyurl.com/sim-bag-data

Code

# Options: 
# data <- read_csv("path/to/where/you/downloaded/it")
# navigate to the file in your file explorer pane. Click on the file and "import dataset"
data <- read_csv("https://tinyurl.com/sim-bag-data")
head(data)

# A tibble: 6 × 5
  `Flight Number` `Tail Number` `Origin Airport` Arrival            
  <chr>           <chr>         <chr>            <dttm>             
1 0208            N804UA        ATL              2024-01-23 22:47:00
2 0208            N804UA        ATL              2024-01-23 22:47:00
3 0208            N804UA        ATL              2024-01-23 22:47:00
4 0208            N804UA        ATL              2024-01-23 22:47:00
5 0208            N804UA        ATL              2024-01-23 22:47:00
6 0208            N804UA        ATL              2024-01-23 22:47:00
# ℹ 1 more variable: bag_completion_time <dttm>

2 Inspecting Data

Code

data |> ggplot(aes(x = Arrival)) +
  geom_histogram(binwidth=60*60*3, color = "black") +
  labs(
    title = "Histogram of Plane Arrival Times",
    x = "Arrival Time",
    y = "Count of Planes? Bags? What?"
  ) +
  theme_minimal()

Initial Observations

Arrivals don’t seem to pick up until noon and go constant until 3 AM…hmmm
Could EWR have 20k flights / day? (14 flights/minute)…hmmm

Timezones

Everything is done in POSIX (Unix) time
“It measures time by the number of non-leap seconds that have elapsed since 00:00:00 UTC on 1 January 1970, the Unix epoch.”
UTC is Coordinated Universal Time, not to be confused with Greenwich Mean Time (GMT)
UTC is based on International Atomic Time (TAI) which is a weighted average of the time kept by over 450 atomic clocks in over 80 national laboratories worldwide.

Code

# set timezones so the datetime will DISPLAY correctly
data <- data |> mutate(
          Arrival = as.POSIXct(Arrival, tz = "EST")) |>
        mutate(
          bag_completion_time = as.POSIXct(bag_completion_time,
          tz = "EST"))

kable(head(data))

Flight Number	Tail Number	Origin Airport	Arrival	bag_completion_time
0208	N804UA	ATL	2024-01-23 17:47:00	2024-01-23 18:12:48
0208	N804UA	ATL	2024-01-23 17:47:00	2024-01-23 18:19:04
0208	N804UA	ATL	2024-01-23 17:47:00	2024-01-23 18:10:56
0208	N804UA	ATL	2024-01-23 17:47:00	2024-01-23 18:15:42
0208	N804UA	ATL	2024-01-23 17:47:00	2024-01-23 18:09:44
0208	N804UA	ATL	2024-01-23 17:47:00	2024-01-23 18:10:13

Fixed Histogram

Code

flight_arrivals <- data |>
  distinct(`Flight Number`, Arrival)

ggplot(flight_arrivals, aes(x = Arrival)) +
  geom_histogram(binwidth=60*60*3, fill = "lightblue", color = "black") + # Binwidth = 1 hour (3600 seconds)
  labs(
    title = "Histogram of Plane Arrival Times",
    x = "Arrival Time",
    y = "Count of Planes"
  ) +
  theme_dark()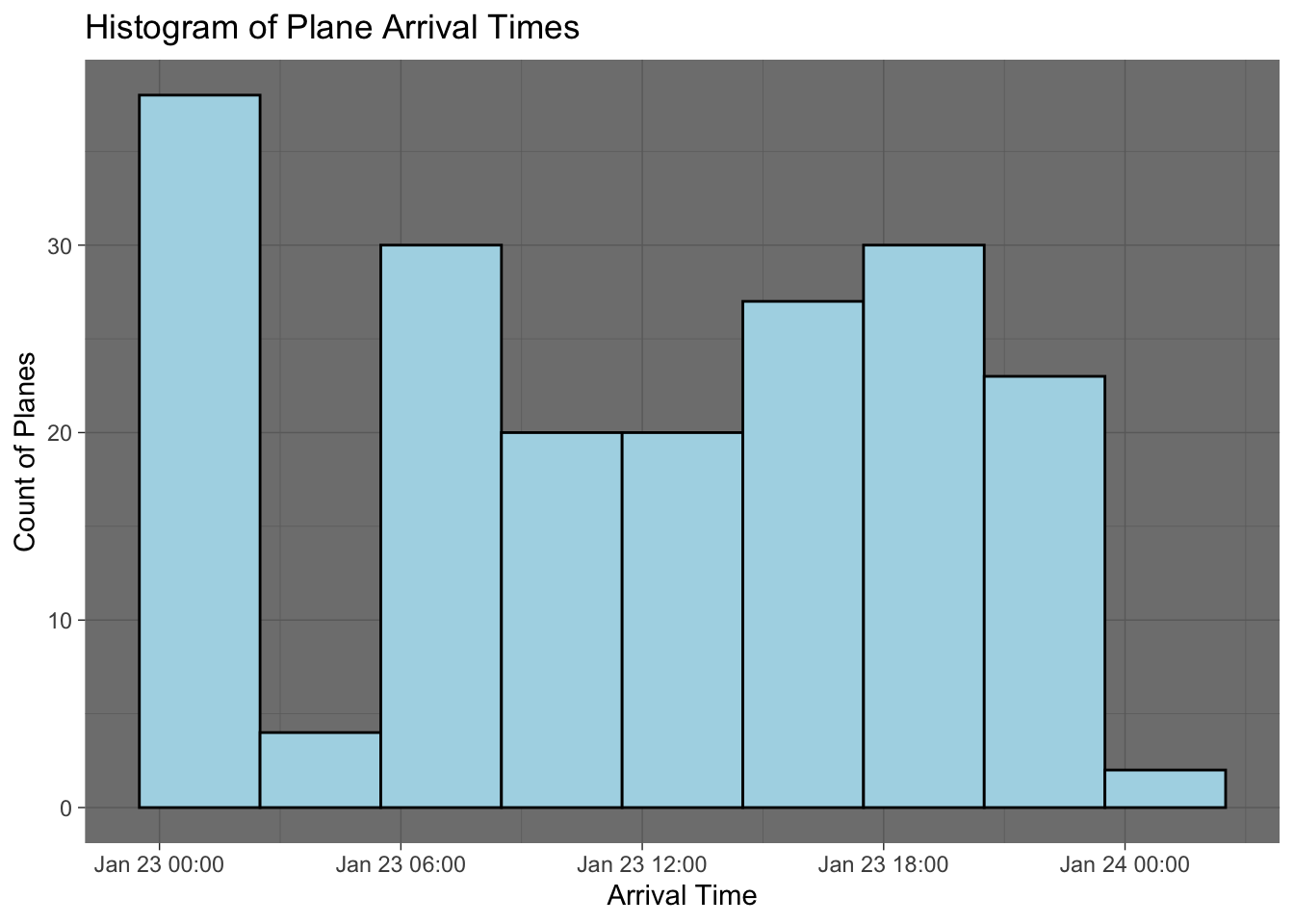

3 Solution

Bag Delivery Time Statistics

What is a statistic?

Code

x_bar <- mean(data$bag_delivery_time)
s <- sd(data$bag_delivery_time)

Does this meet specifications

Code

summary(data)

 Flight Number      Tail Number        Origin Airport    
 Length:19495       Length:19495       Length:19495      
 Class :character   Class :character   Class :character  
 Mode  :character   Mode  :character   Mode  :character  
                                                         
                                                         
                                                         
    Arrival                       bag_completion_time             
 Min.   :2024-01-23 00:00:00.00   Min.   :2024-01-23 00:16:37.00  
 1st Qu.:2024-01-23 06:53:00.00   1st Qu.:2024-01-23 07:21:11.00  
 Median :2024-01-23 12:14:00.00   Median :2024-01-23 12:52:01.00  
 Mean   :2024-01-23 11:39:42.83   Mean   :2024-01-23 12:09:40.24  
 3rd Qu.:2024-01-23 18:22:00.00   3rd Qu.:2024-01-23 18:51:19.50  
 Max.   :2024-01-23 23:47:00.00   Max.   :2024-01-24 00:31:43.00

3.1 Visualize Data

Code

data <- data |> mutate(bag_delivery_time = as.numeric(bag_completion_time - Arrival))

data |> ggplot(aes(x = bag_delivery_time)) + 
  geom_histogram()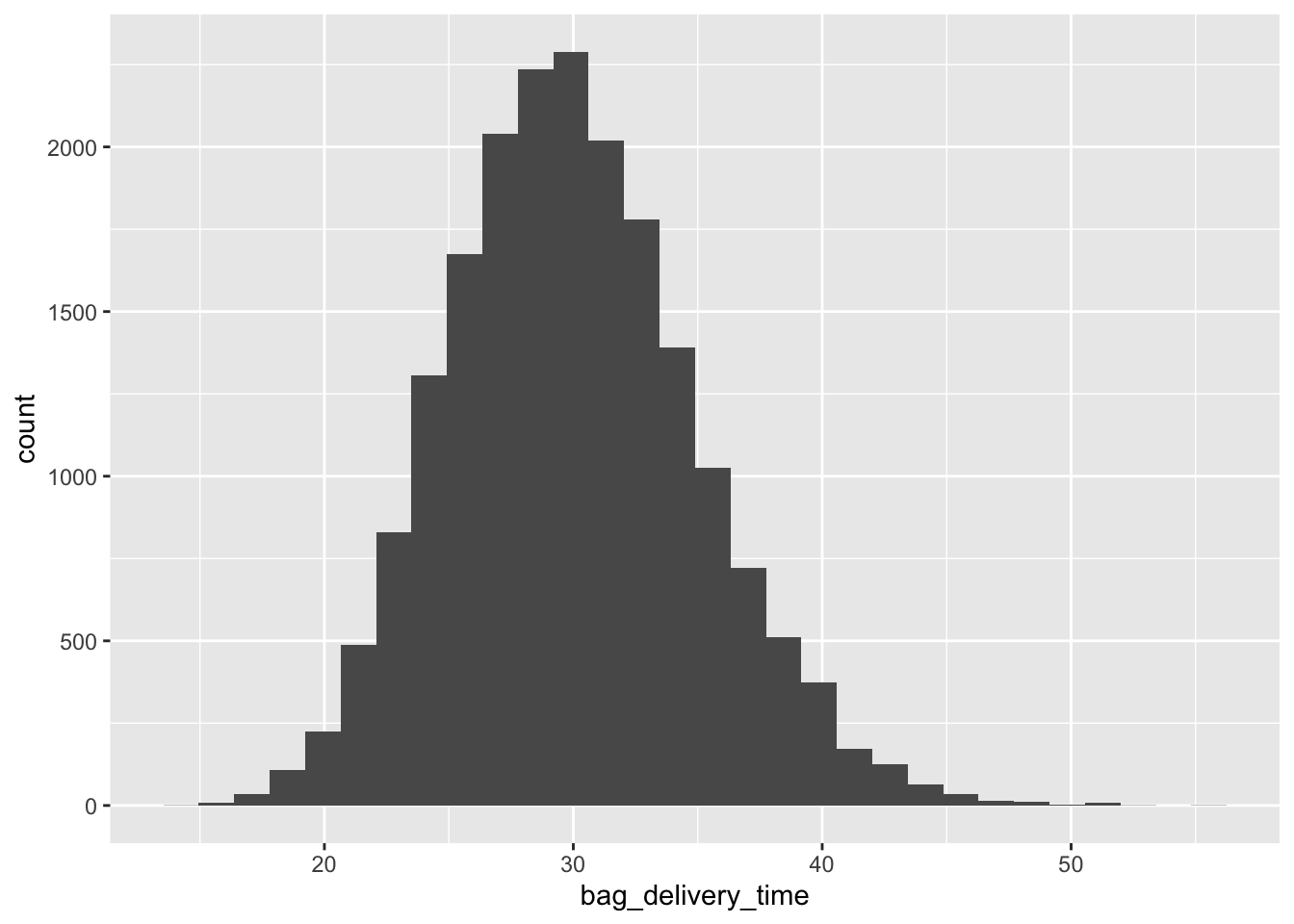

3.2 Fit Distributions to Data

use fitdistrplus to fit various distributions

Code

f_norm <- fitdist(data$bag_delivery_time, "norm")
f_ln <- fitdist(data$bag_delivery_time, "lnorm")
f_weibull <- fitdist(data$bag_delivery_time, "weibull")
f_gamma <- fitdist(data$bag_delivery_time, "gamma")

plot.legend <- c("Normal", "LogNormal", "Weibull", "Gamma")

use plotting functionality to plot a comparison of the data.

Code

denscomp(
  list(f_norm, f_ln, f_weibull, f_gamma),
  xlab = "Bag Delivery Time (min)",
  legendtext = plot.legend)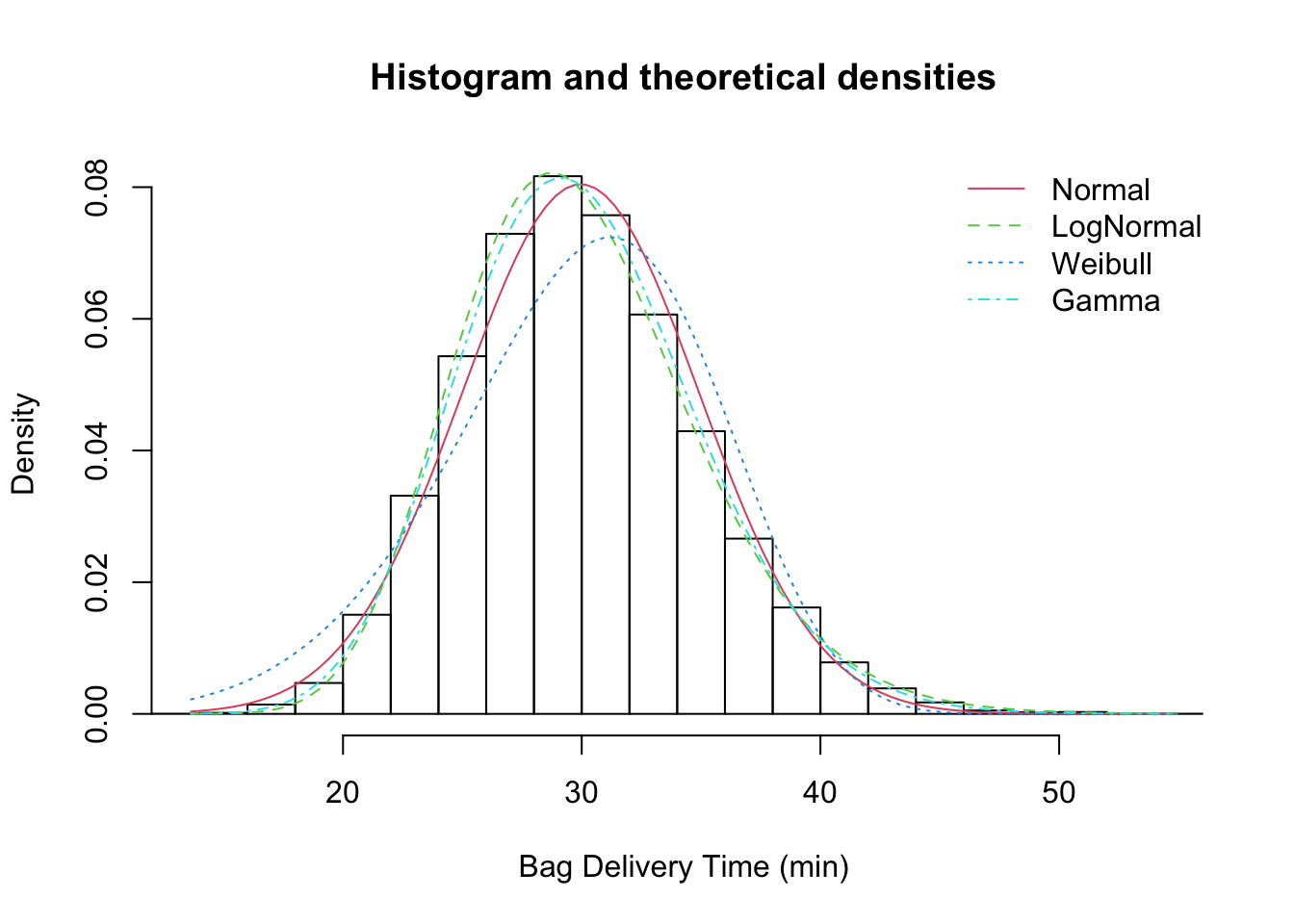

3.3 Compare to Manual Apporach

Alternatively, can generate probabilities for each bag arrival time by applying the fitted distributions to the data

Code

data <- data |> mutate(
  Weibull = dweibull(bag_delivery_time,
                      shape = f_weibull$estimate["shape"],
                      scale = f_weibull$estimate["scale"]),
  Normal = dnorm(bag_delivery_time,
                      mean = f_norm$estimate["mean"],
                      sd = f_norm$estimate["sd"]),
  Gamma = dgamma(bag_delivery_time,
                      shape = f_gamma$estimate["shape"],
                      rate = f_gamma$estimate["rate"]),
  LogNormal = dlnorm(bag_delivery_time,
                      meanlog = f_ln$estimate["meanlog"],
                      sdlog = f_ln$estimate["sdlog"]),
)

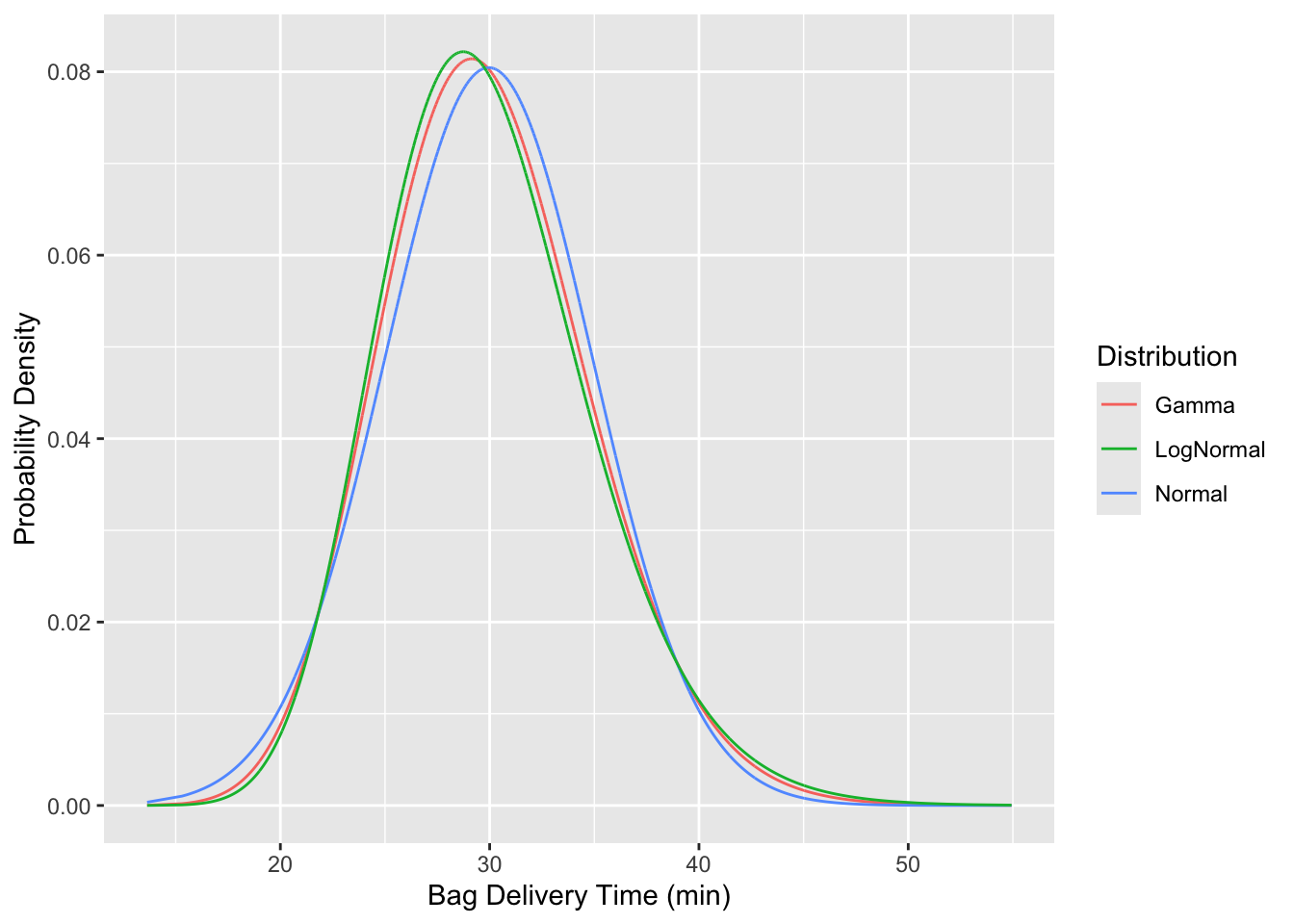
Then can plot these direclty one at a time

Code

data |> ggplot(aes(x = bag_delivery_time)) +
  geom_line(aes(y = Gamma, color="Gamma", line="grey")) +
  geom_line(aes(y = Normal, color="Normal")) +
  geom_line(aes(y = LogNormal, color="LogNormal")) +
  labs(
    color = "Distribution",
    x = "Bag Delivery Time (min)",
    y = "Probability Density"
  )

Alternatively, we could transform our tidy data from “wide” to “long” form

Code

long_data <- data |> pivot_longer(
  cols = c(Gamma, LogNormal, Normal, Weibull),
  names_to = "Distribution",
  values_to = "Probability")

Using kable to output a formatted table.

Code

kable(head(long_data))

Flight Number	Tail Number	Origin Airport	Arrival	bag_completion_time	bag_delivery_time	Distribution	Probability
0208	N804UA	ATL	2024-01-23 17:47:00	2024-01-23 18:12:48	25.80000	Gamma	0.0632560
0208	N804UA	ATL	2024-01-23 17:47:00	2024-01-23 18:12:48	25.80000	LogNormal	0.0666378
0208	N804UA	ATL	2024-01-23 17:47:00	2024-01-23 18:12:48	25.80000	Normal	0.0566180
0208	N804UA	ATL	2024-01-23 17:47:00	2024-01-23 18:12:48	25.80000	Weibull	0.0480593
0208	N804UA	ATL	2024-01-23 17:47:00	2024-01-23 18:19:04	32.06667	Gamma	0.0687913
0208	N804UA	ATL	2024-01-23 17:47:00	2024-01-23 18:19:04	32.06667	LogNormal	0.0661965

and we can actually plot this much easier

Code

ggplot() +
  # Histogram or density plot of `bag_delivery_time`
  geom_histogram(data = data, aes(x = bag_delivery_time, y = ..density..), 
                 bins = 30, color="black", fill = "skyblue", alpha = 0.5) +
  # Overlay probability density lines from `long_data`
  geom_line(data = long_data, aes(x = bag_delivery_time, y = Probability, color = Distribution), size=1)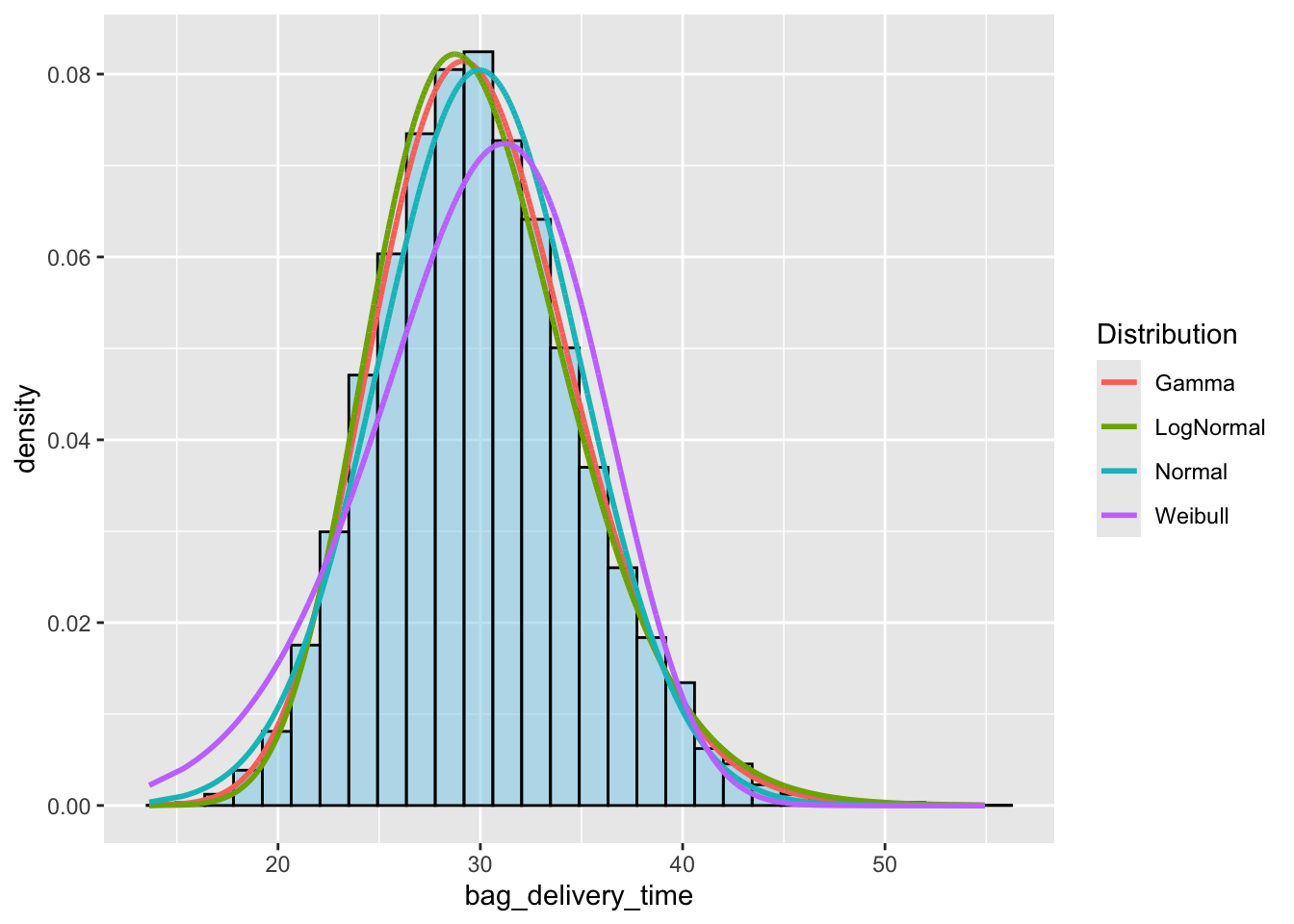

For relativley simple scenarios, it may be easier to manually plot the data yourself
As data and plots become more sophisticated this can be difficult
I recommend getting familiar with “long” and “wide” data and how to go between the two.

3.4 Conclusion

Which distribution is the best fit?
How do you know?
Does the schematic design meet specifications?

Code

#| echo: true

fitted_distributins <- list(f_gamma, f_ln, f_norm, f_weibull)

# Extract summary metrics from the fitted distributions
summary_table <- sapply(fitted_distributins, function(fit) {
  c(
    "Number of Parameters" = as.integer(length(fit$estimate)),  # Number of parameters
    "Log-Likelihood" = fit$loglik,                # Log-likelihood
    "AIC" = fit$aic,                              # Akaike Information Criterion
    "BIC" = fit$bic                               # Bayesian Information Criterion
  )
})

# Convert to a data frame for readability
# summary_table <- as.data.frame(summary_table)

# Assign column names based on your distributions
colnames(summary_table) <- c("Gamma", "Log-Normal", "Normal", "Weibull")  # Adjust based on distribution names

# View the table
kable(summary_table)

	Gamma	Log-Normal	Normal	Weibull
Number of Parameters	2.00	2.00	2.00	2.0
Log-Likelihood	-58690.38	-58732.54	-58877.11	-59819.8
AIC	117384.75	117469.09	117758.23	119643.6
BIC	117400.51	117484.84	117773.98	119659.3