#5 Queuing using Simmer

14:540:384: Simulation Models in IE (Spring 2025)

Author
Affiliation

Daniel Moore

Rutgers University

Published

2025-02-19

Questions

1 Review

  1. Shown why we need simulations and a few practical examples
  2. Discussed where distributions come from, how to get them and how to use them
  3. Shown how to manipulate data and create visualizations
  4. Demonstrated two coding patterns for simulations

2 Learning Objectives

  1. Problem analysis
  2. Set up a simple simulation with simmer
  3. Run the simulation and extract results

3 Problem

Revisit the Wholefoods Return queue

  • customers arrive at a rate \(\lambda = 3/min\)
  • single server with exponential service time with \(\mu = 1/2min\)
  • run this simulation for 4 hours

4 Implementation

  • simmer: a process-oriented and trajectory-based Discrete-Event Simulation (DES) package for R
  • Allows us to define the essentials of our system
  • It handles the simulation part as well as extracting metrics and nice visualizations

4.1 Loading Packages

# usual suspects
library(tidyverse)
library(knitr)
library(fitdistrplus)

# new kid on the block
library(simmer)
library(simmer.plot)
library(simmer.bricks)

4.2 Defining Model

# all given in minutes
lambda <- 1/3
mu <- 1/2
t_f <- 4*60

RV_arr <- function(n=1) {
  rexp(n, rate = lambda)
}

RV_service <- function(n=1) {
  rexp(n, rate = mu)
}

4.3 Simmer Components

  • Environment: The simulation environment, which contains the resources and processes

  • Trajectories: The paths that entities take through the simulation, which define the sequence of events that occur

  • Resources: The resources that are used in the simulation, such as servers, buses, and waiting areas

Let’s break the problem down into components

4.3.1 Customer Trajectory

cust_traj <- trajectory() |>
  seize("clerk", 1) |>
  timeout(function() RV_service(1)) |>
  release("clerk", 1)
  • Very basic trajectory. Customer shows up, gets in line (if necessary), makes a return, and leaves as shown in @plot-customer-trajectory
plot(cust_traj)
  • some bug I’ll investigate and demonstrate next time how to get the plot to appear correctly.

4.3.2 More complex trajectory

More complex plotted trajectory from the docs

4.3.3 Instantiating the Simulation Environment

return_line <- simmer() |>
  add_resource("clerk", 1) |>
  add_generator("customer", cust_traj, function() RV_arr(1))

4.4 Running the Simulation

return_line |> run(t_f)
simmer environment: anonymous | now: 240 | next: 240.785768094172
{ Monitor: in memory }
{ Resource: clerk | monitored: TRUE | server status: 1(1) | queue status: 1(Inf) }
{ Source: customer | monitored: 1 | n_generated: 87 }

4.5 Getting Results

get_mon_resources: gets information about the “server” usage get_mon_arrivals: gets information about the “customers”

4.5.1 Resource Visualization

resources <- get_mon_resources(return_line)

kable(head(resources))
  • averages over time:
plot(resources, metric = "usage")

System usage over time
  • instantaneous usage:
plot(resources, metric = "usage", steps=TRUE)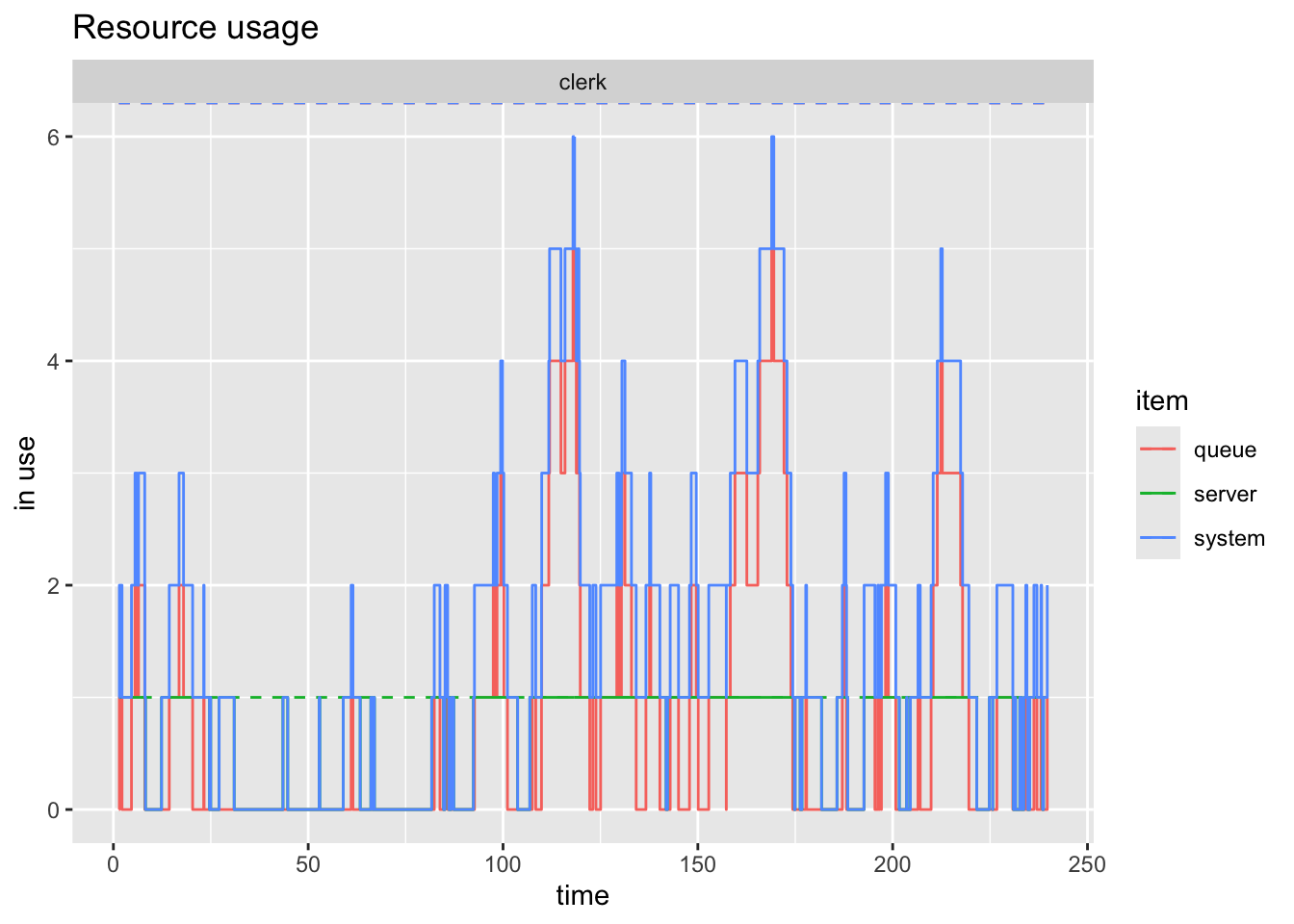

System usage over time
  • utiliazation of the resources. Not super interesting here due to only one resource
plot(resources, metric = "utilization")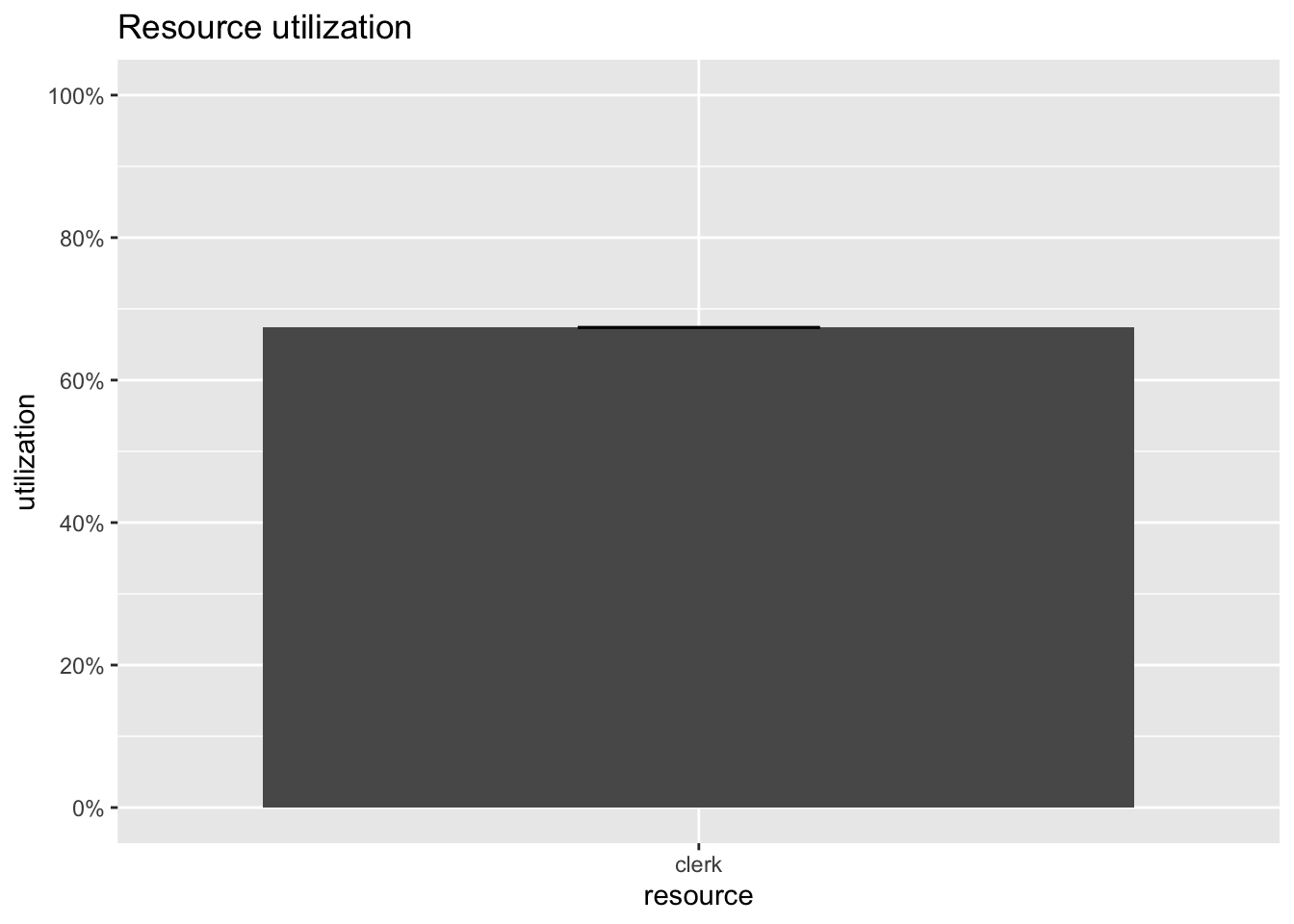

System utilization over time
  • looking at just the queue
plot(resources, metric = "usage", items="queue", steps=TRUE)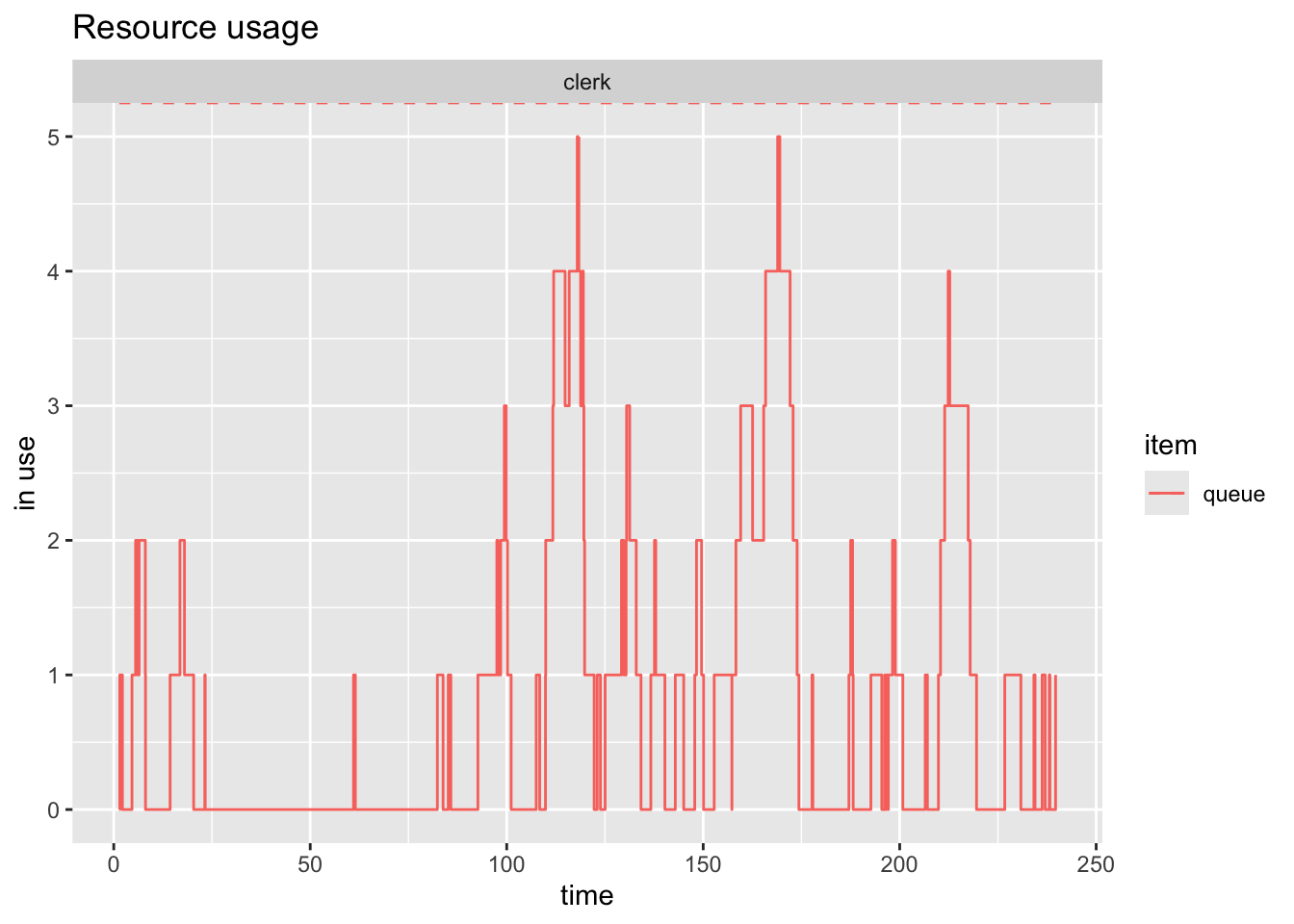

Queue usage over time
plot(resources, metric = "usage", items="server", steps=TRUE)

4.5.2 Customer Visualization

arrivals <- get_mon_arrivals(return_line)

kable(head(arrivals))
name start_time end_time activity_time finished replication
customer0 1.415610 2.212143 0.7965332 TRUE 1
customer1 1.537848 6.077795 3.8656514 TRUE 1
customer2 4.641538 8.041888 1.9640935 TRUE 1
customer3 5.554621 8.082859 0.0409708 TRUE 1
customer4 6.454990 8.230710 0.1478507 TRUE 1
customer5 12.354493 18.001193 5.6467005 TRUE 1 
plot(arrivals, metric = "activity_time")
`geom_smooth()` using method = 'loess' and formula = 'y ~ x'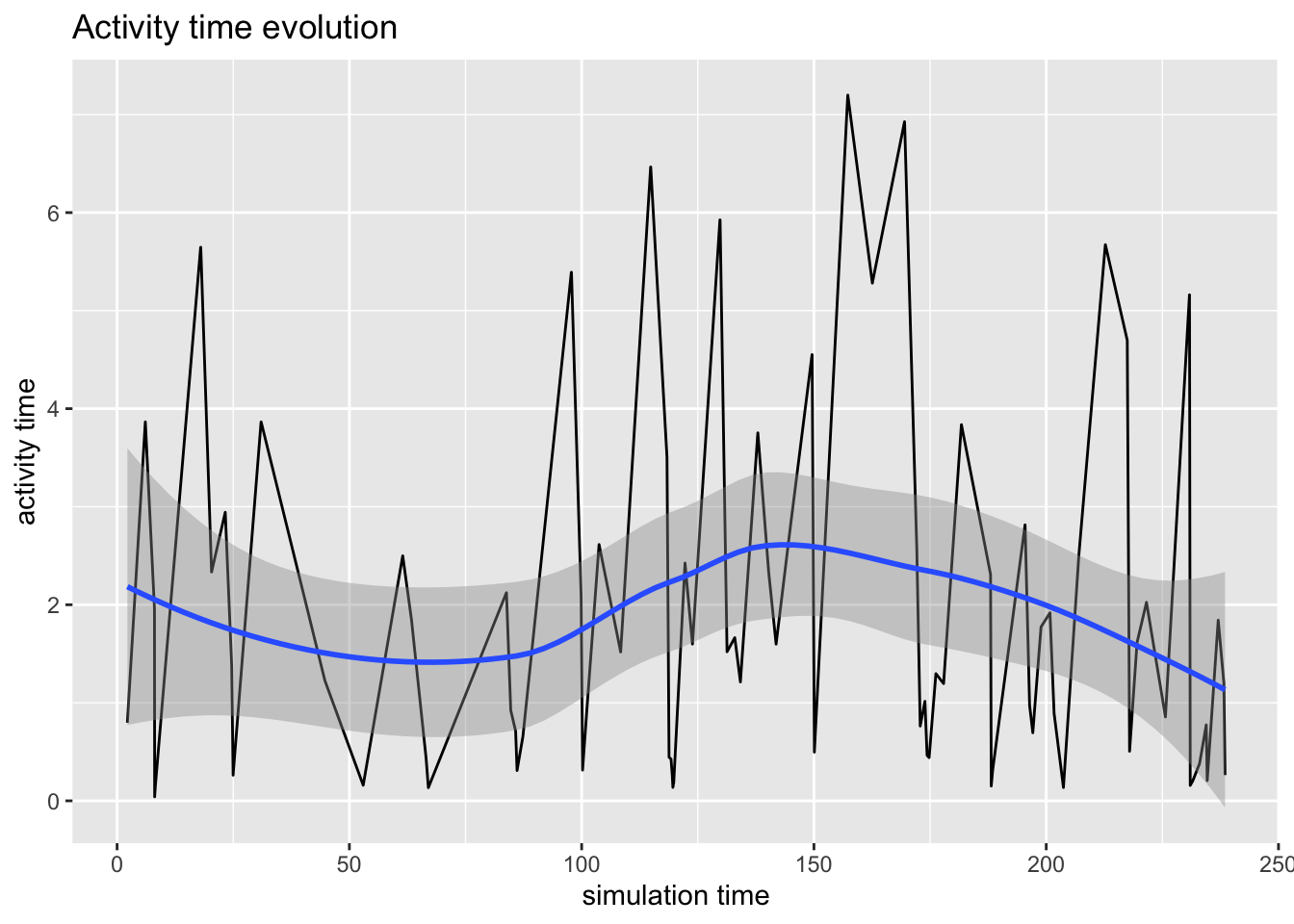

Activity time of customers
plot(arrivals, metric = "waiting_time")
`geom_smooth()` using method = 'loess' and formula = 'y ~ x'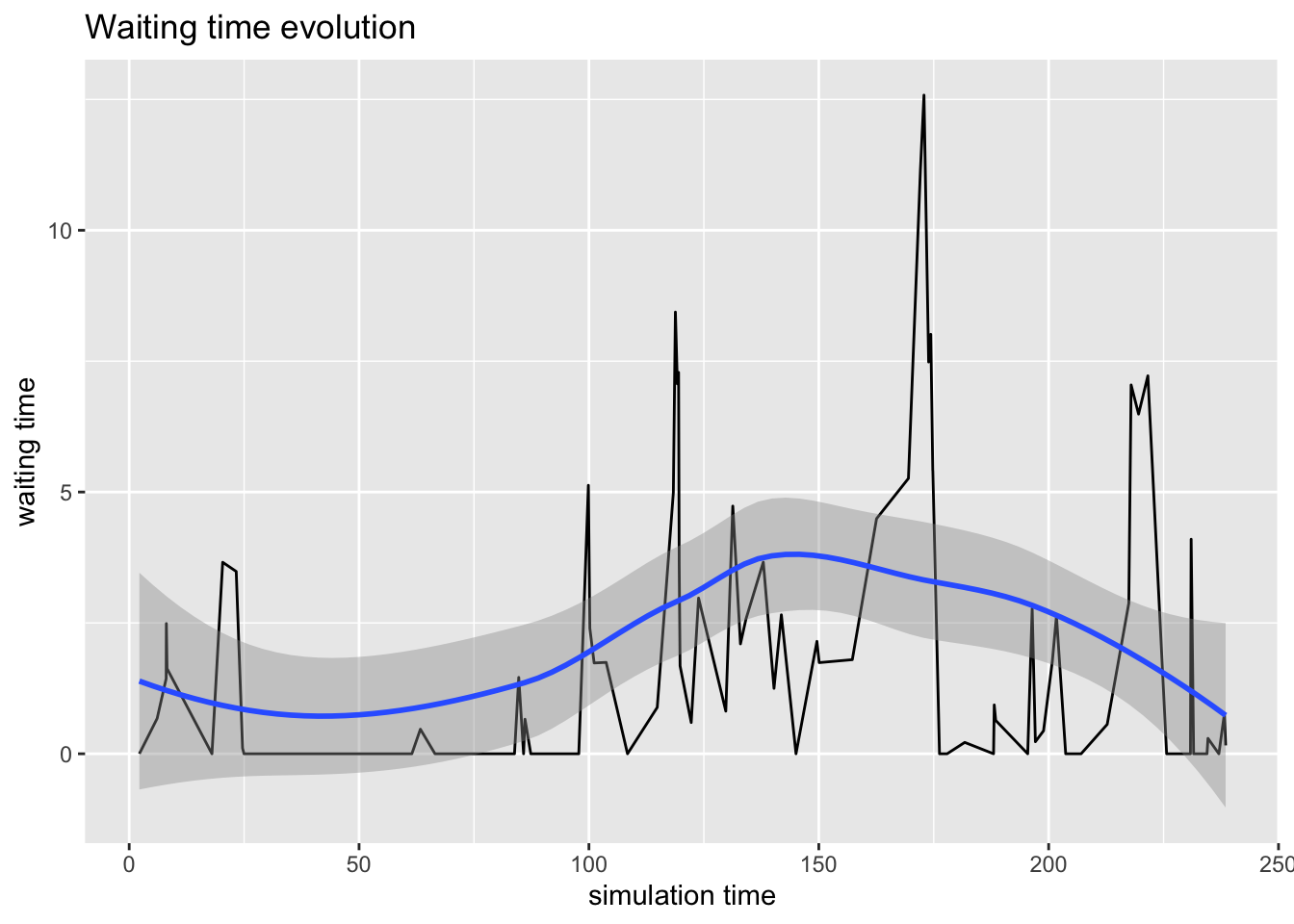

Wait time of customers
plot(arrivals, metric = "flow_time")
`geom_smooth()` using method = 'loess' and formula = 'y ~ x'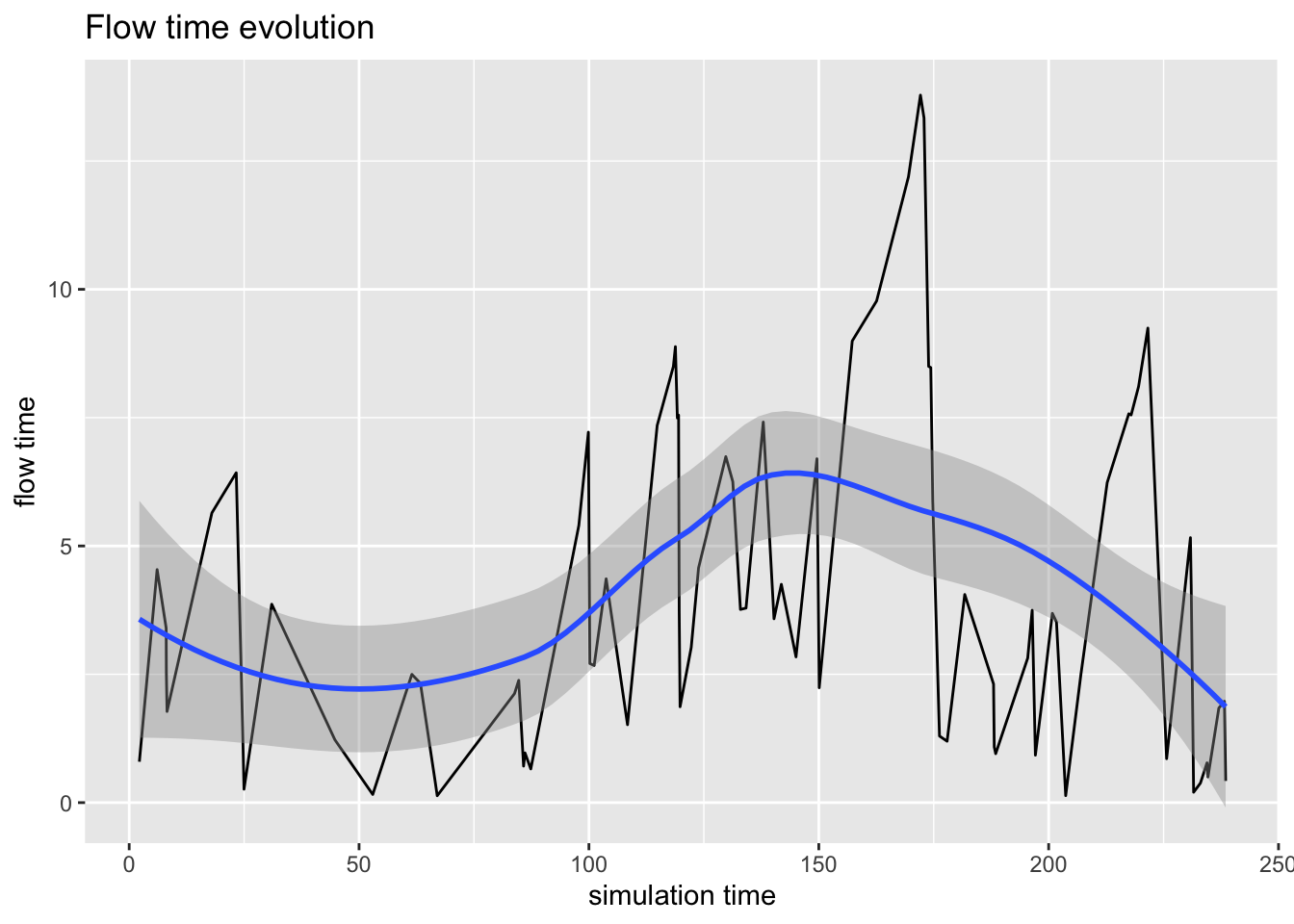

Flow time of customers

5 Conclusion

  • Simmer is a powerful tool for building and simulating discrete event systems
  • Once we can define the components and dynamics we can build a simulation
  • We can visualize the model we’ve built to make sure it matches our expectations
  • All the details are handled for us

6 Next Steps

  • Working with our own distributions
  • More complex systems such as:
  • different paths
  • different servers
  • different customers